Causality in Machine Learning 101 for Dummies like Me
Recently I started wondering how Causal inference is being used with machine learning and especially wherein the data science project
lifecycle? I have been researching this for a while, discussed with
colleagues and finally came to the conclusion that Causal inference can
be used after the modeling phase in order to confirm some correlations
between variables and the target/outcome. For example, if the model has
good accuracy and gives you a high correlation/association between input
A and the target B you may want to perform a causal inference to validate
that A has an effect on
B. But then I ponder whether that’s all
Causality can help me achieve or is there some other application of
Causality in Machine learning.
But to be really honest finding correlations between variables is simple but turning them into causal assertions needs an extra effort. Causal inference is used mostly to reach a prescription in the form of do X so that Y happens. Causality seems to be the core interest of the scientific community when we think about relationships between different entities, variables, and concepts in life. “Why” is the ultimate question when we explore nature and her interactions with the ecosystem.
“Why” suggest that we live in “black box” that contains self-consciousness. Which “sphere” will it pass through, how are the thoughts influenced and what structures will be formed after passing through the “sphere”?
What is Causal Inference?
When you work with historical data or you can only observe the data without affecting it, causal inference comes into play. Generally, causal inference is a controversial topic as it tries to extract causal relations from observational data(as opposed to experimental data in A/B tests). In most machine learning projects these types of experiments are possible and mostly cheap, therefore why bother? Moreover, especially in predictive projects, value comes from correlated relations. Knowledge of causal relations, which are a subset of correlated relations, does not add value. Now, let us say we would like to dive in causal reasoning. First things first, one might ask what kind of questions are causal? In fact, they are not farfetched and we face them in our every day lives. Questions such as:
Image Source: https://towardsdatascience.com/introducing-dowhy-cc58b75d61ac
- “Would the ad on my website get more clicks had its background color been red instead of blue?” or
- “Would my FB newsfeed look much more like the way I want it to, had I answered FB’s survey questions?” or
- “Would my blood pressure be lower had I consumed less salt?” or
- “What if I consumed whey protein instead of creatine after a workout, would I gain more muscle?” or
- “Would I not get lung cancer had I not smoked?”

…and many more are the types of causal questions. The first question asks about the causal effect of background color on ad clicks, the second about the causal effect of answering survey questions on the quality of one’s FB news feed, the third about causal effect of salt on high blood pressure, the fourth about the causal effect of supplements on muscle gain in workout, and the fifth about the causal effect of smoking on lung cancer. In general, many “what if” questions which ask about what would have happened had we taken some alternative action comparing with what we already did, have a causal sense. Answering these questions requires moving beyond association and undertaking the mathematics of causal reasoning, a deed that is fortunately ongoing in the state-of-the-art research in artificial intelligence and other disciplines of science such as statistics, epidemiology, economics, etc.
When not to use Causal Inference
If it is possible to do experiments, causal inference can be avoided.
For example, A/B tests let you study the effect of a change in two
groups and reach a causal conclusion. For example, the result of an A/B
test would be “users in group A which see a button with color intensity
50 clicked 10% more than group B with color intensity 40”, so do:
X=increase color intensity of the button, so that;
Y=more click happens.
With larger, more uniform groups, your assertion would be more reliable.
The three-layer Causal Hierarchy
A useful insight unveiled by the theory of causal models is the classification of causal information in terms of the kind of questions that each class is capable of answering. This classification forms a 3-level hierarchy in the sense that questions at level i (i = 1, 2 ,3 ) can only be answered if information from level j (j ≥ i) is available.
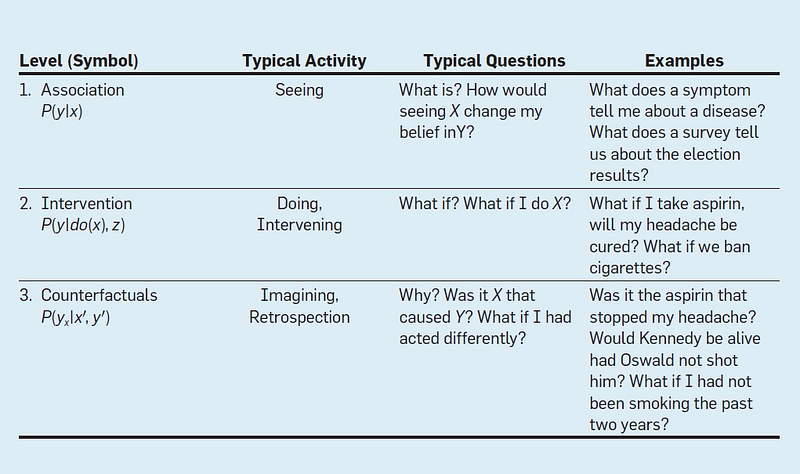
The lowest (first) layer is called Association and it involves purely statistical relationships defined by the naked data. This is the layer at which most machine learning systems operate.
Level two, Intervention involves not just seeing what is, but reasoning about the effects of actions you might take(interventions). I would argue that reinforcement learning systems operate at this level (e.g., ‘what will happen if I move my knight to this square?’). RL systems tend to operate in very well defined environments though, whereas the intervention layer envisioned here encompasses much more open challenges too. As an example of an intervention, Pearl provides the question “What will happen if we double the price?” (of an item we are selling).
Such questions cannot be answered from sales data alone, because they involve a change in customers behaviour, in reaction to the new pricing.
Personally, I would have thought that if we had sales data showing the effects of previous price increases(on the same or similar items) then it might well be possible to build a predictive model from that data alone. Pearl’s counter-argument is that unless we replicate precisely the market conditions that existed the last time the price reached double its current value, we don’t really know how customers will react).
The highest level of causal reasoning is called counterfactuals and addresses what if? questions requiring retrospective reasoning. On a small scale, this is what I see sequence-to-sequence generative models being capable of doing. We can ‘replay’ the start of a sequence, change the next data values, and see what happens to the output.
The levels form a hierarchy in the sense that interventional questions
cannot be answered from purely observational information, and
counterfactual questions cannot be answered from purely interventional
information (e.g., we can’t re-run an experiment on subjects who were
given a drug to see what would have happened had they not been given
it).
The ability to answer questions at level j though implies that we can
also answer questions at level (i≤ j)
This hierarchy, and the formal restrictions it entails, explains why machine learning systems, based only on associations, are prevented from reasoning about actions, experiments, and causal explanations.
How to Solve Causal Inference?
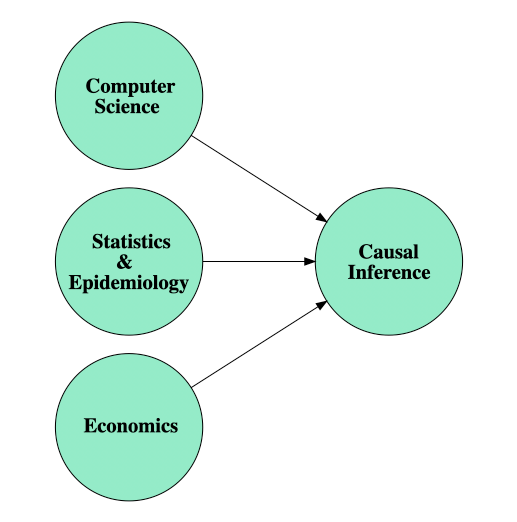
The science of causal reasoning has roots and is developing, in various disciplines, notably philosophy (going back to as old as Aristotle), epidemiology, economics, statistics, computer science, etc. Currently, two of the notable well-established frameworks that provide solid mathematical infrastructures for causal reasoning are the following:
- Structural Causal Models (SCM) developed by Judea Pearl which enables us to infer causality via Directed Acyclic Graphs (DAG). The mathematics of intervention, a necessary component for inferring causality, is provided in SCMs through the “do-operator.” When assessing whether X is causing Y, one learns, through this framework, that in general, Pr(Y=y|X=x)≠ Pr(Y=y|do(X=x)), where do(X) denotes an intervention on the random variable X and Pr(.) denotes the probability of a random variable (note that here, I only considered whether X is causing Y, such relationship is asymmetric in a causal sense and hence, whether Y causes X needs a separate causal analysis). The left-hand side of the formula above points to conditional probabilities (not causal in general), whereas elucidation of a causal relationship between variables requires incorporation of intervention (right-hand side of the formula) and using the mathematics of the “do-calculus.”
- The “potential outcomes” framework formulated and developed by Donald Rubin (and originally proposed by Jerzy Neyman), professor of statistics at Harvard, which is commonly referred to under the names of Rubin Causal Model (RCM), or the Rubin-Neyman causal model. In order to elucidate whether X causes Y, this framework, speaking at a high level, contrasts the potential outcomes (Y) of an interventional experiment in which a data point (say, an individual) is exposed to different levels of X. For example, if we are to examine the causal effect of Advil on headache, we would contrast the outcomes (whether one has a headache) of an interventional experiment treating (taking Advil) and controlling (not taking Advil). The gold standard experiment for finding such a contrast of outcomes is a Randomized Controlled Trial (RCT), but RCTs are not always feasible. The details of experimental design, as well as those of how to infer causality in the absence of RCTs, is out of the scope of this article, but I would be more than happy to discuss further with interested readers.
The two frameworks, the SCM and the RCM, use two fairly different “representations” (if I may) and sets of assumptions for causal reasoning, but at the end of the day, are axiomatically translatable to each other and eventually serve the same goal, which is extracting causal relationships between variables. Despite the availability of such well-established frameworks, causal reasoning in artificial intelligence has not matured yet and many difficult challenges are unresolved. Many of the current AI systems are, in general, incapable of such ability. Fortunately, however, several AI researchers, including groups like ours at Pennsylvania State University, are actively working in this area. I hope that with causal reasoning, AI systems would improve much more and would be able to help solve more complex real-world problems.
Reinforcement Learning & Causality
In recent years, the machine learning research community has expressed growing interest in both fields. This interest in reinforcement learning has been fueled by significant achievements in combining deep learning and reinforcement learning to create agents capable of defeating human experts. Prominent examples include the ancient strategy game Go and team-based competitions in the fantasy computer game Dota 2. Some think deep reinforcement learning is the path to generalized AI.
Speaking of playing games, human agents “play” the “game” of living life by forming causal models of their environment. These are conceptual models (“this is a baseball, that is a window”) with causal relationships between objects (“if I throw the baseball at the window, it will shatter”). Causal models allow us to transfer knowledge to new unfamiliar situations (“I bet if I throw this weird new hard heavy thing at that strange new brittle glassy thing, it will also break”).
Humans reason with these models when deciding what actions to perform and not to perform. Have you ever thought about your actions in a given situation and thought, “had I done things differently, things would have turned out better.” That is called counterfactual regret, and it is a form of causal reasoning. You use a model of cause-and-effect in your head to mentally simulate how things would have played out if you had made different decisions. Counterfactual regret is the difference between this simulated would-be outcome and the outcome that actually played out. You are making use of powerful cognitive machinery when you make decisions you believe will avoid regretful outcomes based on causal reasoning about past decision-making.
Some game-playing agents, such as the one that recently defeated human poker experts in no-limit Texas hold’em, do a brute-force version of minimizing counterfactual regret by simulating millions of games. This relies on far more experience and computing resources than a human player. Commercial applications of deep reinforcement learning are virtually non-existent, except for the massive amounts of money dumped into OpenAI and Deepmind so they can play video games (nothing wrong with that).
However, the core theory in RL is the same theory that powers various elements of decision science; sequential experimentation, optimization, decision theory, game theory, auction design, etc. Applying these branches of theory to decision problems is precisely where data scientists have had the most impact, especially in tech.
Causal modeling is the thread that connects all of these fields. It even brings in computational cognitive psychology, where one model, the causal models humans have in their heads. This allows one to model human irrationality, like cognitive biases and fallacies, from data on how their behavior. In my eyes, advertisers spend a great deal of time getting people to spend their money irrationally.
Conclusion
The nature of causality is really hard. The paradox is that we use it continuously on a daily basis, it is common sense in a lot of cases, but finding a definition assessing in which cases A causes B in the real world is very difficult! We would all agree that raining causes the floor wet (I hope… we may find rain deniers, too). But how do we give a clear definition that distinguishes between the rain or the air is the cause of the wetness? How do we know that rain is the main cause and not another unobserved variable that causes rain and the floor wet at the same time? Ponder that as much as you’d like…In the eighteenth century, David Hume had already started to think about the nature of causality, and many philosophers have written about it.
The general agreement in the statistics community is that you cannot prove a causal effect at least without performing an experiment. When you deal with observational data (data obtained passively, without you experimenting), the most you can expect is to talk about correlation (probabilistic dependency). This has created a scenario where talking explicitly about causality in observational data is taboo.
Even though proving causality in such cases is not possible, there are benefits of talking about causality explicitly. The first one is easy to understand: most of our knowledge as humans about how the world works is observational. You don’t make experiments about all the things you know. In some cases, it is not even possible: does the sun cause daylight? how do you make an experiment about it, switching the sun on and off? in this case, you could try some type of surrogate experiment and argue that this validates the original hypothesis, but it is not straightforward either. Meanwhile, we all agree that the sun causes daylight. The second argument is to avoid misleadingness. When you analyze data is because you won’t arrive at some conclusions to take further actions. If you think in that way, it is because you think those actions affect (and thus are a cause of) some quantity of interest. So, even you talk about correlations for technical correctness, you are going to use those insights in a causal way. So, if your objective is a causal one, you’d better talk explicitly.
Reference
- Simpson’s paradox is an entry point to become interested in causal inference.
- The Seven Tools of Causal Inference with Reflections on Machine Learning
- From Dependency to Causality: A Machine Learning Approach
- Causal Data Science: A nine-part series on Medium by Adam Kelleher
- Interpreting linear models from a causal perspective: “ Graphical Tools for Linear Structural Equation Modeling”, Bryant Chen and Judea Pearl
- “Causal Inference in Statistics: A Primer”, (DAGs framework) Pearl J., Glymour M., and Jewell N.P.
- “Causal Inference”, (Potential Outcomes framework) Hernán M.A. and Robins J.M.
- “Mostly Harmless Econometrics: An Empiricists Companion”, (Econometrics point of view) Angrist J.D. and Pischke J.