Game Theory 101 for Dummies like Me

Game Theory is one of the most fascinating branches of mathematics with tons of applications to fields ranging from the social sciences to the biological sciences. Game Theory has even found its way into mainstream media through movies such as A Beautiful Mind,with Russell Crowe. This post may end up becoming a little thought-provoking towards the end, but I tried to justify the title, as best as I could.
What is a “Game”?
Game Theory is the study of “games.” Games, in the mathematical sense, are defined as strategic situations in which there are multiple participants. Furthermore, the outcome of the decision any individual makes is dependent on the decision that anindividual’s decision and the decisions made by all of the other participants.
**Is Sudoku a “game?”
**No, not the way we defined “game.” Sudoku is not a “game” because what
you do when solving the game is independent of what anyone else does.
Is Chess a “game?”
**Yes! Imagine that you are playing a game of chess with a friend.
Whether you win or not will be dependent on the moves you make
**andthe moves your friend makes. At the same time, whether or not
they win will be dependent on the moves they make andthe moves you
make.
NOTE:The most important thing to realize in the chess example is that at least 2 “participant’s” decisions were affected by the decisions of other participants. Solving a Sudoku puzzle is not a game since how you solve the puzzle is not affected by anyone else’s decisions.
Ok, I get what a “game” is, but what is Game Theory?
Game Theory is the study of “games.” Game theorists try to model “games” in a way that makes them easy to understand and analyze. A lot of “games” end up having similar properties or reoccurring patterns, but sometimes it is hard to understand a complicated game.
Let’s work through an example of a game from a scene of Governing Dynamics: Ignore the Blonde — A Beautiful Mind and how a game theorist might model it.
The Problem
You and three male friends are at a bar trying to pick up women.
Suddenly one blonde and four brunettes enter in a group. What’s the
individual strategy?
Here are the rules. Each of you wants to talk to the blonde. If more
than one of you tries to talk to her, however, she will be put off and
talk to no one. At that point, it will also be too late to talk to a
brunette, as no one likes being the second choice. Assume anyone who
starts out talking to a brunette will succeed.
The Movie
Nash suggests the group should cooperate. If everyone goes for the blonde, they block each other and no one wins. The brunettes will feel hurt as a second choice and categorically reject advances. Everyone loses.
But what if everyone goes for a brunette? Then each person will succeed, and everyone ends up with a good option.
It’s a good thought, except for one question: what about the blonde?
The Equilibrium
The movie is directed so well that it sounds persuasive. But it’s sadly incomplete. It misses the essence of non-cooperative game theory.
A Nash equilibrium is a state where no one person can improve, given what others are doing. This means you are picking the best possible action in response to others–the formal term is you are picking the best response.
As an example, let’s analyze whether everyone going for a brunette is a Nash equilibrium. You are giventhat q``1three of your friends go for brunettes. What is your best response?
You can either go for the brunette or the blonde. With your friends already going for brunettes, you have no competition to go for the blonde. The answer is clear that you would talk to the blonde. That’s your best response. Incidentally, this is a Nash equilibrium. You are happy, and your friends cannot do better. If your friends try to talk to the blonde, they end up with nothing and give up talking to a brunette. So you see, when Nash told his friends to go for the brunettes in the movie, it really does sound like he was leaving the blonde for himself.
The Lesson
The advice that sounds good for you might really be better for someone else. Be skeptical of the strategic implications.
Now, in practical matters, it will be hard to achieve the equilibrium that only one person goes for a blonde. There is going to be competition and someone in the group will surely sabotage the mission. So there are two ways you might go about it using strategies outside the game. One is to ignore the current group and wait for another group of blondes (the classic “wait and see” strategy). The second is to let a random group member go for the blonde as the others distract the brunettes (also practiced as “wingman theory”).
What else can Game Theory DO?
Game theory as we already know is the study of how and why people make decisions within a competitive situation while keeping in mind what actions their competitors will take. You can think of it as the study of strategic decision making.
But, game theory isn’t just about games. It’s used for any situation where two people have to make decisions with rewards and consequences. The ultimate goal is to find whether a “best” strategy for a given game exists.
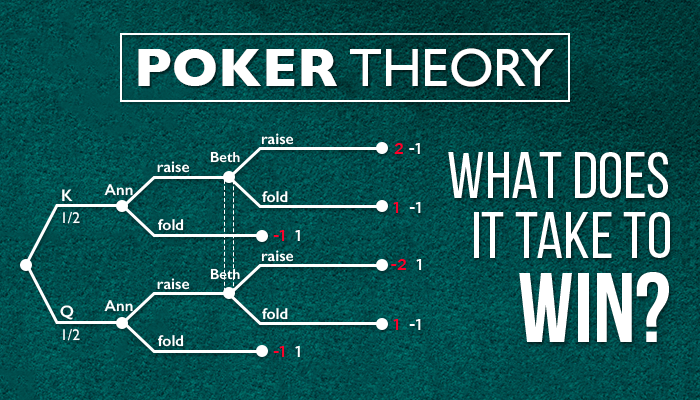
Poker is a great example because the other player’s choices influence your strategy. For example, should you play tight while your opponent is playing loose? Or, should you bluff or not? Or, raise/fold?
To further understand game theory, here are some of the more important concepts:
- Prisoner’s Dilemma — refers to a situation where two completely rational individuals might not cooperate, even if it appears that it’s in their best interests to do so. Classic choice between self-interest and mutual interest.
- Coordination game — a game in which the players benefit from working together. There’s no incentive for either party to cheat since it will result in a worse outcome than cooperating. Example: driving on the right side of the road.
- Free Rider Problem (Tragedy of the Commons) — a problem in which every individual tries to reap the greatest benefit from a given resource, which harms others who can no longer enjoy the benefits. Examples: pollution, over-fishing, and ocean garbage.
- Zero-Sum — the situation in which one person or group can win something only by causing another person or group to lose it. Examples: poker and gambling
- Principal-Agent Problem — when one person (the agent) is allowed to make decisions on behalf of another person (the principal). In this situation, the agent will not prioritize the best interest of the principal, but will instead pursue his own goals. Ex: politics
- Nash Equilibrium — an optimal outcome where no player has an incentive to deviate from his chosen strategy after considering an opponent’s choice. Ex: traffic lights
- Grim Trigger — a strategy employed in a repeated non-cooperative game where you start by cooperating and continue to cooperate as long as everyone has cooperated in the past. If someone has defected, then you defect forever.
- Schelling Points — a solution that people will tend to use in the absence of communication because it seems natural, special, or relevant to them. Example: meeting at noon at Grand Central
- Keynesian Beauty Contest — an analogy for investing that suggests that investors may guess what other investors are going to think as opposed to what they think themselves.
- Bounded Rationality — when given a choice, people will always follow a path that is simple and something they are used to (even if it’s not the most optimal outcome).
- Byzantine Generals Problem — the situation where parties must agree on a single strategy in order to avoid complete failure, but where some of the involved parties are corrupt and disseminating false information or are otherwise unreliable. (This problem is built around an imaginary General who makes a decision to attack or retreat and must communicate the decision to his lieutenants. A given number of these actors are traitors & they cannot be relied upon to properly communicate orders.)

What economists call Game Theory psychologists calls the theory of social situations, which is an accurate description of what game theory is about. Although game theory is relevant to parlor games such as poker or bridge, most research in game theory focuses on how groups of people interact. There are two main branches of game theory: cooperative and noncooperative game theory. In addition to game theory, economic theory has three other main branches:
Decision Theory
It can be viewed as a theory of one-person games or a game of a single player against nature. The focus is on preferences and the formation of beliefs. The most widely used form of decision theory argues that preferences among risky alternatives can be described by the maximization of the expected value of a numerical utility function, where utility may depend on a number of things, but in situations of interest to economists often depends on money income. Probability theory is heavily used in order to represent the uncertainty of outcomes, and Bayes Law is frequently used to model the way in which new information is used to revise beliefs. Decision theory is often used in the form of decision analysis, which shows how best to acquire information before making a decision.
General Equilibrium Theory
It can be viewed as a specialized branch of game theory that deals with trade and production, and typically with a relatively large number of individual consumers and producers. It is widely used in the macroeconomic analysis of broad-based economic policies such as monetary or tax policy, in finance to analyze stock markets, to study interest and exchange rates and other prices. In recent years, the political economy has emerged as a combination of general equilibrium theory and game theory in which the private sector of the economy is modeled by general equilibrium theory, while voting behavior and the incentive of governments are analyzed using game theory. Issues studied include tax policy, trade policy, and the role of international trade agreements such as the European Union.
Mechanism Design Theory
It differs from game theory in that game theory takes the rules of the game as given, while mechanism design theory asks about the consequences of different types of rules. Naturally, this relies heavily on game theory. Questions addressed by mechanism design theory include the design of compensation and wage agreements that effectively spread risk while maintaining incentives, and the design of auctions to maximize revenue or achieve other goals.
The Principles Of Game Theory
Most game theory models involve the following five conditions:
- Each decision-maker has two or more choices or sequences of choices (“plays”).
- All possible combinations of decisions or plays result in a clear outcome: win or lose.
- The scenarios have a well-defined outcome and decision-makers receive a “payoff (the value of the outcome to the participants). That is, participants will gain or lose something depending on the outcome.
- The decision-makers know the rules of the game as well as the payoffs of the other decision-makers.
- The decision-makers are rational: when faced with two alternatives, players will choose the option that provides the greatest benefits.
While decision-makers know the rules and their opponents’ options, they do not know their opponent’s actual decisions in advance. Hence, decision-makers must choose options based on assumptions of what their opponents will choose. Some game theory scenarios are also zero-sum games, meaning that one decision-maker wins what another loses. Others, however, allow mutual gains and losses. Moreover, these scenarios or games involve several strategies: minimizing the maximum losses another decision-maker can cause and making decisions based on probability.

In addition, games and scenarios admit different degrees of information. Perfect information games such as chess and checkers contain no surprises: each player has a finite number of moves and each player sees the opponent’s moves and can respond to them immediately. But other games and scenarios, such as the Prisoner’s Dilemma, contain surprises and more guesswork.
Economist John Harsanyi postulated that in differential or asymmetric games (even including chess, checkers, etc.), each player is certain about only his own utility function, but must speculate about other players’ utility functions and, more importantly, other players’ conception of every other players’ utility functions. Simply put, each player must know his own payoff probability, guess other players’ payoff probabilities, and also guess what other players’ are guessing about his own payoff probability. Furthermore, the player must guess what other players are guessing about his guesses about them, forming an infinite regress.
Importance of Game Theory in Economics
1. Game theory shows the importance of duopolists in finding some way to agree. It helps to explain why duopoly prices tend to be administered in a rigid way. If prices were to change often, tacit agreements would not be found and would be difficult to enforce.
2. Game theory also highlights the importance of self-interest in the business world. In-game theory, self-interest is routed through the mechanism of economic competition to bring the system to the saddle point. This shows the existence of a perfectly competitive market.
3. Game theory tries to explain how the duopoly problem cannot be determined. For this, it uses the solution without saddle point under constant-sum-two-person game. At the same time, the duopoly problem without a saddle point is solved by allowing each firm to adopt mixed strategies on a probability basis. In this way, the duopoly problem is shown to be always determined.
4. Further, game theory has been used to explain the market equilibrium when more than two firms are involved. The solution lies in either collusion or non-collusion. These are known as cooperative non-constant-sum game and non-cooperative non-constant-sum game respectively.
5. “Prisoner’s Dilemma” in game theory points towards collective decision making and the need for cooperation and common rules of the road.
6. A player in game theory may be regarded as a single person or an organization in the real world subject to decision making with a certain amount of resources. The strategy in game theory is a complete specification of what a player will do under each circumstance in the playing of the game. For example, the Director of a firm might tell his sales staff how he wants an advertising campaign to start and what should they do subsequently in response to various actions of competing firms.
Image Source: https://xkcd.com/601/
7. The importance of the pay-off values lies in predicting the outcome of a series of alternative choices on the part of the player. Thus a perfect knowledge of the pay-off matrix to a player implies perfect predictions of all factors affecting the outcome of alternative strategies. Moreover, the minimax principle shows to the player the next course of action which would minimize the losses if the worst possible situation arose.
8. Again, game theory is helpful in solving the problems of business, labor, and management. As a matter of fact, a businessman always tries to guess the strategy of his opponents so as to implement his plans more effectively. Similar is the case of management in trying to solve the problem of the labor union’s bargaining for higher wages. Management might adopt the most profitable counter-strategy to tackle such problems. Further, producers might make decisions in which the estimation of profits was to be balanced against the cost of production.
9. Last but not least, there are certain economic problems that involve risk and technical relations. They can be handled with the help of the mathematical theory of games. Problems of linear programming and activity analysis can provide the main basis for economic application of the theory of games.
Limitations of Game Theory
- Though Game Theory offers many benefits, it cannot be applied in all situations. There are instances where rationality or diplomacy might not offer the solutions one is looking for. There are instances where mutual benefit might not be the most ideal outcome. During situations like this, one has to make the conscious decision of whether or not to use Game Theory to settle issues.
- Also, there is no hard and fast rule that the settlement reached using Game Theory should end with a mutual benefit. Though the theory adds structure and clarity to the negotiation, there are elements of uncertainty that might favor one party over the other.
- The assumption that both parties are going to be rational and cooperate with each other to reach a mutual agreement can prove to be risky. The theory assumes that both parties won’t be hell-bent on their self-interests while it may not be the case.
Real-World Examples of Game Theory
There are multiple real-life examples for understanding the basic concept of game theory. Let us take up a simple one: Apple and Samsung involved in a ‘game of advertising’. As both firms have a stable market reputation, the advertising costs are a direct drain on the net corporate profits.
If both do not advertise, their profits will remain the same (with many simplistic assumptions, including that there are no other competitors).
But advertising budgets are assigned in both the firms so that they do not lose market share to the competitor (spending on advertising is a good strategy for both irrespective of the decision taken by the competitor).
The same analogy can be comfortably replicated for the US-USSR cold war, in which both the nations seemed to be hell-bent on adding more nukes in their arsenal.
Another common example that we see in everyday life is related to public goods: if all the residents of society decide to become good citizens and decide not to throw trash in the open — the society benefits as a whole (even the property rates might go up!).

But an individual might behave in a rogue way (selfish?) by throwing
trash in the open — the cost of cleaning is borne by the whole society.
This also extends to the free-rider
problem and tragedy
of commons.
Game theory has a variety of applications in diverse fields — economics,
business, political science, biology, computer science, and even
philosophy. It has helped and is currently helping strategists of
every kind all over the world to better design their environments, to
suit their overall needs.
Conclusion
We are constantly ‘in the game’ — our life is impacted by the actions and decisions made by others. And here is a thought that might as well be the ultimate philosophical rhetoric originating from game theory: “We can create a better world by becoming better human beings ourselves”.